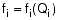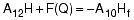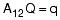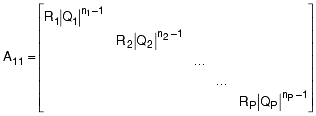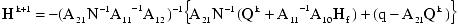Given a network defined by N unknown head nodes, P links of unknown flow, and B boundary or fixed head nodes, the network topology can be expressed in two incidence matrices:

and

The following convention is used to assign matrix values:

Assigned nodal demands are given by:

Assigned boundary nodal heads are given by:

The headloss or gain transform is expressed in the matrix:

These matrix elements that define known or iterative network state can be used to compute the final steady-state network represented by the matrix quantities for unknown flow and unknown nodal head.

Unknown link flow quantities are defined by:

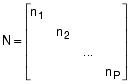
Unknown nodal heads are defined by:

These topology and quantity matrices can be formulated into the generalized matrix expression using the laws of energy and mass conservation:

A second diagonal matrix that implements the vectorized head change coefficients is introduced. It is generalized for Hazen-Williams friction losses in this case:

This yields the full expression of the network response in matrix form:

To solve the system of non-linear equations, the Newton-Raphson iterative scheme can be obtained by differentiating both side of the equation with respect to Q and H and get:

with

The final recursive form of the Newton-Raphson algorithm can now be derived after matrix inversion and various algebraic manipulations and substitutions (not presented here). The working system of equations for each solution iteration, k, is given by:

The solution for each unknown nodal head for each time iteration is computationally intensive This high-speed solution utilizes a highly optimized sparse matrix solver that is specifically tailored to the structure of this matrix system of equations.

Sources:

Todini, E. and S. Pilati, "A gradient Algorithm for the Analysis of Pipe Networks," Computer Applications in Water Supply, Vol. 1-Systems Analysis and Simulation, ed. By Bryan Callback and Chin-Hour Or, Research Studies Press LTD, Watchword, Hertfordshire, England.